By Geunu Jeong, Head of SwiftMR Research at AIRS Medical
SwiftMR is a deep learning-based product that enhances the quality of MR images. So, how does this algorithm differ from existing deep learning algorithms to achieve such outstanding reconstruction performance? You can find the answer in the paper “All-in-One Deep Learning Framework for MR Image Reconstruction” published by AIRS Medical on arXiv. Although the content is technically challenging, let’s try to understand it step by step!
When an MRI scan is performed, raw data called k-space data is obtained first. Each point in the k-space data is referred to as a sample. The number of samples and the noise level of each sample in the k-space data vary depending on the scan parameters set. When the scan parameters are set to use longer scan time, more samples can be obtained, each with a lower noise level. Whereas, under the scan parameters set for shorter scan time, fewer samples must be obtained, each with a higher noise level. After a series of mathematical operations, this k-space data is transformed into an MR image that reveals the structure of our body. The quality of the image depends on the number of samples in the k-space data and the noise level of each sample.
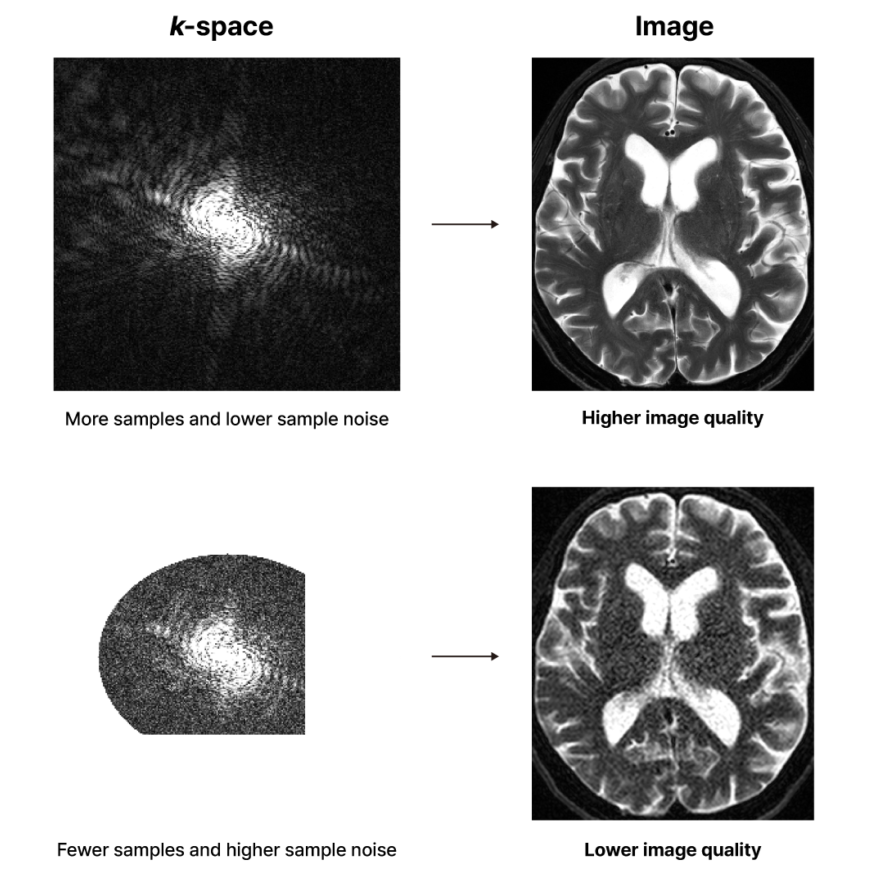
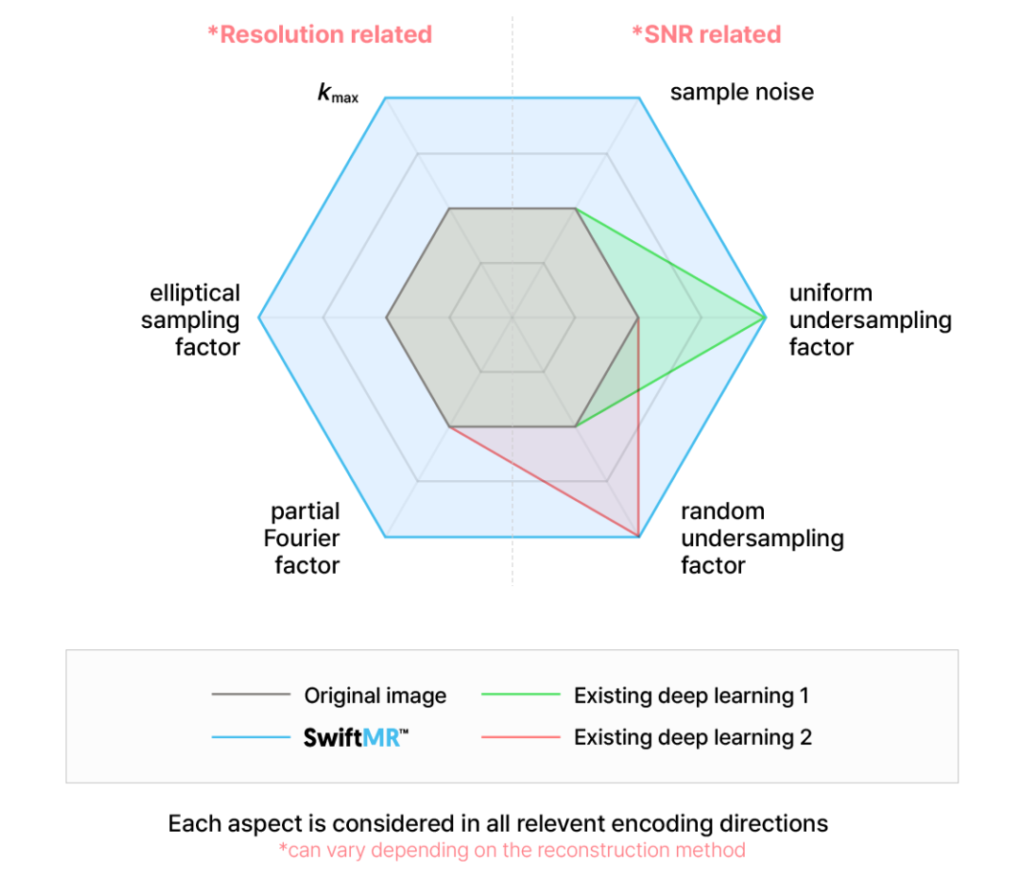
Improving MR image quality through a deep learning algorithm essentially means transforming an image into ‘one that is created from k-space obtained with a larger number of samples and a lower level of sample noise’. Let’s take a closer look at the “a larger number of samples” part. There are several ways to acquire more k-space samples: sampling more densely (lower uniform/random undersampling factor), extending sampling range (higher kmax), sampling in a larger elliptical shape (higher elliptical sampling factor), and sampling more symmetrically (higher partial Fourier factor). Each of these methods affects image quality in a different mathematical way and is independent of the others; in other words, they cannot replace one another. For example, while both extending sampling range and sampling more symmetrically share the common benefit of enhancing perceived resolution, extending sampling range does not mitigate the blurring caused by asymmetric sampling.
“The key to SwiftMR’s deep learning algorithm’s performance lies in
achieving image quality improvement in all these aspects simultaneously.”

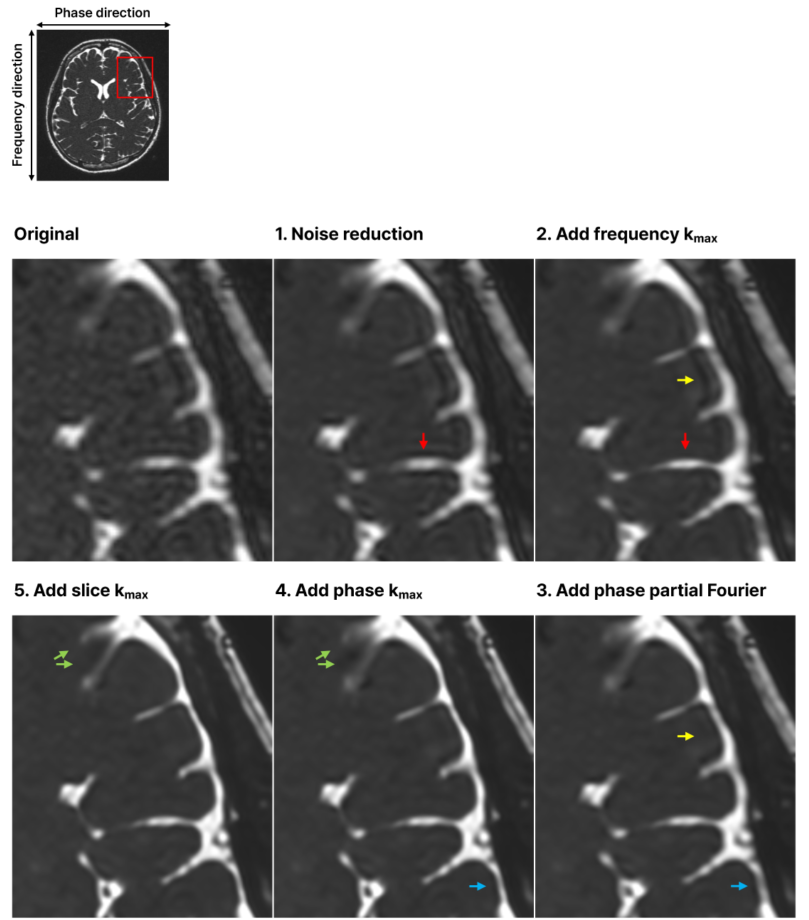
To demonstrate this, we processed the same image multiple times, each time sequentially incorporating an additional improvement aspect, and then observed the changes. The reconstructed images at each step are illustrated in the figure below. In Image 1, only the improvement of k-space sample noise is considered. Image 2 additionally includes extending sampling range in the frequency direction. Image 3 further adds sampling more symmetrically in the phase direction. Image 4 also incorporates extending sampling range in the phase direction. Lastly, Image 5 adds extending sampling range in the slice direction. Each step showed image quality enhancement corresponding to the newly added aspect. By comparing the original image with the fully SwiftMR-processed Image 5, the achievement of multi-dimensional image quality improvement is evident. Other aspects were excluded from the example figure below because they were already at their maximum in the original image.
So far, we have introduced the secret to SwiftMR’s remarkable performance, which is multi-dimensional image quality enhancement. The combination of quality improvements across these various aspects results in exceptional enhancements in resolution and SNR. This is where SwiftMR differs from most existing deep learning algorithms, which improve image quality in only one aspect (uniform/random undersampling factor). So, how was the deep learning training done to achieve such multi-dimensional improvements in image quality? Detailed explanations can be found in the paper at https://arxiv.org/abs/2405.03684!